حل الصيغ آلة حاسبة على الانترنت. المعادلات
المعادلات
كيفية حل المعادلات؟
في هذا القسم سوف نتذكر (أو ندرس، اعتمادًا على من تختاره) المعادلات الأساسية. إذن ما هي المعادلة؟ في اللغة البشرية، هذا نوع من التعبير الرياضي حيث توجد علامة يساوي ومجهول. والذي يشار إليه عادة بالحرف "X". حل المعادلة- هذا هو العثور على قيم x التي يتم استبدالها بها إبداعيالتعبير سوف يعطينا الهوية الصحيحة. اسمحوا لي أن أذكرك أن الهوية هي تعبير لا شك فيه حتى بالنسبة لشخص غير مثقل بالمعرفة الرياضية على الإطلاق. مثل 2=2، 0=0، ab=ab، وما إلى ذلك. فكيف حل المعادلات؟دعونا معرفة ذلك.
هناك كل أنواع المعادلات (أنا متفاجئ، أليس كذلك؟). ولكن يمكن تقسيم كل تنوعها اللامتناهي إلى أربعة أنواع فقط.
4. آخر.)
كل الباقي، بالطبع، الأهم من ذلك كله، نعم...) وهذا يشمل التكعيبي، الأسي، اللوغاريتمي، المثلثي وجميع أنواع الآخرين. وسنعمل معهم بشكل وثيق في الأقسام المناسبة.
سأقول على الفور أنه في بعض الأحيان تكون معادلات الأنواع الثلاثة الأولى مشوشة للغاية لدرجة أنك لن تتعرف عليها حتى... لا شيء. وسوف نتعلم كيفية الاسترخاء لهم.
ولماذا نحتاج إلى هذه الأنواع الأربعة؟ ثم ماذا المعادلات الخطيةحلها بطريقة واحدة مربعآحرون، الكسر الكسرى - الثالث،أ استراحةإنهم لا يجرؤون على الإطلاق! حسنًا، لا يعني ذلك أنهم لا يستطيعون اتخاذ القرار على الإطلاق، بل إنني كنت مخطئًا في الرياضيات.) الأمر فقط أن لديهم تقنيات وأساليب خاصة بهم.
ولكن لأي (أكرر - ل أي!) توفر المعادلات أساسًا موثوقًا وآمنًا للحل. يعمل في كل مكان ودائما. كريم الأساس هذا - يبدو مخيفًا، لكنه بسيط جدًا. و جدا (جداً!)مهم.
في الواقع، يتكون حل المعادلة من هذه التحولات ذاتها. 99% أجب على السؤال: " كيفية حل المعادلات؟" يكمن بالتحديد في هذه التحولات. هل التلميح واضح؟)
التحويلات المتطابقة للمعادلات.
في أي معادلاتللعثور على المجهول، تحتاج إلى تحويل وتبسيط المثال الأصلي. وهكذا عندما يتغير المظهر جوهر المعادلة لم يتغير.تسمى هذه التحولات تطابقأو ما يعادلها.
لاحظ أن هذه التحولات تنطبق على وجه التحديد للمعادلات.هناك أيضًا تحولات في الهوية في الرياضيات التعبيرات.هذا موضوع آخر
الآن سوف نكرر كل شيء، كل شيء، كل شيء أساسي تحويلات متماثلة للمعادلات.
أساسية لأنه يمكن تطبيقها عليها أيالمعادلات - الخطية، التربيعية، الكسرية، المثلثية، الأسية، اللوغاريتمية، إلخ. وما إلى ذلك وهلم جرا.
التحول الأول للهوية: يمكنك إضافة (طرح) إلى طرفي أي معادلة أي(لكنه واحد!) رقم أو تعبير (بما في ذلك تعبير بمجهول!). وهذا لا يغير جوهر المعادلة.
بالمناسبة، كنت تستخدم هذا التحويل باستمرار، وكنت تعتقد أنك تنقل بعض الحدود من جزء من المعادلة إلى جزء آخر مع تغيير الإشارة. يكتب:
الحالة مألوفة، نحرك الاثنين إلى اليمين فنحصل على:
![]()
في الواقع أنت تم استبعاده او تم اخذهمن طرفي المعادلة اثنان. والنتيجة هي نفسها:
س+2 - 2 = 3 - 2
إن تحريك المصطلحات إلى اليسار واليمين مع تغيير الإشارة هو ببساطة نسخة مختصرة من تحويل الهوية الأول. ولماذا نحتاج إلى هذه المعرفة العميقة؟ - أنت تسأل. لا شيء في المعادلات في سبيل الله تحمليه. فقط لا تنسى تغيير العلامة. لكن في حالات عدم المساواة، يمكن لعادة التحويل أن تؤدي إلى طريق مسدود...
تحويل الهوية الثانية: يمكن ضرب طرفي المعادلة (تقسيمها) على نفس الشيء غير صفريةرقم أو تعبير وهنا يظهر بالفعل قيد مفهوم: الضرب في الصفر أمر غبي، والقسمة مستحيلة تمامًا. هذا هو التحويل الذي تستخدمه عندما تحل شيئًا رائعًا
انها واضحة X= 2. كيف وجدته؟ بالاختيار؟ أم أنها فجرت عليك للتو؟ لكي لا تختار ولا تنتظر البصيرة، عليك أن تفهم أنك عادل قسمة طرفي المعادلةعلى 5. عند تقسيم الجانب الأيسر (5x)، تم تقليل الخمسة، وترك X خالصًا. وهو بالضبط ما نحتاجه. وعند قسمة الطرف الأيمن من (١٠) على خمسة، يكون الناتج بالطبع اثنين.
هذا كل شئ.
إنه أمر مضحك، لكن هذين التحولين المتطابقين (اثنتين فقط!) هما أساس الحل جميع معادلات الرياضيات.رائع! من المنطقي أن ننظر إلى أمثلة ماذا وكيف، أليس كذلك؟)
أمثلة على التحويلات المتماثلة للمعادلات. المشاكل الرئيسية.
دعنا نبدء ب أولاًتحول الهوية. نقل اليسار واليمين.
قدوة للصغار.)
لنفترض أننا بحاجة إلى حل المعادلة التالية:
3-2س=5-3س
ولنتذكر التعويذة: "مع X - إلى اليسار، بدون X - إلى اليمين!"هذه التعويذة عبارة عن تعليمات لاستخدام التحويل الأول للهوية.) ما التعبير الذي يحمل علامة X الموجود على اليمين؟ 3x؟ الجواب غير صحيح! على يميننا - 3x! ناقصثلاثة ×! لذلك، عند التحرك إلى اليسار، ستتغير الإشارة إلى علامة زائد. سوف يتحول:
3-2س+3س=5
لذا، تم جمع علامات X في كومة. دعونا ندخل في الأرقام. هناك ثلاثة على اليسار. بأي علامة؟ الجواب "بلا أحد" غير مقبول!) أمام الثلاثة بالفعل لا يوجد شيء مرسوم. وهذا يعني أنه قبل الثلاثة يوجد زائد.لذلك وافق علماء الرياضيات. لا شيء مكتوب، وهو ما يعني زائد.لذلك، سيتم نقل الثلاثي إلى الجانب الأيمن مع ناقص.نحن نحصل:
-2س+3س=5-3
لم يتبق سوى تفاهات. على اليسار - إحضار مماثلة، على اليمين - عد. الجواب يأتي مباشرة:
في هذا المثال، كان تحويل هوية واحد كافيا. ولم تكن هناك حاجة إلى الثانية. حسنًا حسنًا.)
قدوة للأطفال الأكبر سنا.)
إذا أعجبك هذا الموقع...
بالمناسبة، لدي موقعين أكثر إثارة للاهتمام بالنسبة لك.)
يمكنك التدرب على حل الأمثلة ومعرفة مستواك. الاختبار مع التحقق الفوري. دعونا نتعلم - باهتمام!)
يمكنك التعرف على الوظائف والمشتقات.
الغرض من الخدمة. تم تصميم حاسبة المصفوفات لحل أنظمة المعادلات الخطية باستخدام طريقة المصفوفات (انظر مثالاً لحل المشكلات المشابهة).تعليمات. لحلها عبر الإنترنت، تحتاج إلى تحديد نوع المعادلة وتعيين أبعاد المصفوفات المقابلة.
حيث A، B، C هي المصفوفات المحددة، X هي المصفوفة المطلوبة. يتم حل المعادلات المصفوفية من الصيغة (1) و (2) و (3) من خلال المصفوفة العكسية A -1. إذا تم إعطاء التعبير A·X - B = C، فمن الضروري أولاً إضافة المصفوفات C + B وإيجاد حل للتعبير A·X = D، حيث D = C + B (). إذا تم إعطاء التعبير A*X = B 2، فيجب أولاً تربيع المصفوفة B. يوصى أيضًا بالتعرف على العمليات الأساسية على المصفوفات.المثال رقم 1. يمارس. أوجد حل معادلة المصفوفة
حل. دعنا نشير إلى:
ثم ستكتب معادلة المصفوفة بالصيغة: A·X·B = C.
محدد المصفوفة A يساوي detA=-1
بما أن A هي مصفوفة غير مفردة، فهناك مصفوفة معكوسة A -1 . اضرب طرفي المعادلة على اليسار بـ A -1: اضرب طرفي هذه المعادلة على اليسار بـ A -1 وعلى اليمين بـ B -1: A -1 ·A·X·B·B -1 = أ -1 ·ج·ب -1 . بما أن A A -1 = B B -1 = E وE X = X E = X، فإن X = A -1 C B -1
المصفوفة العكسية أ -1: ![]()
لنجد المصفوفة العكسية B -1.
المصفوفة المنقولة B T:
المصفوفة العكسية B -1: ![]()
نحن نبحث عن المصفوفة X باستخدام الصيغة: X = A -1 ·C·B -1 ![]()
إجابة:
المثال رقم 2. يمارس.حل معادلة المصفوفة ![]()
حل. دعنا نشير إلى:
ثم ستكتب معادلة المصفوفة بالصيغة: A·X = B.
محدد المصفوفة A هو detA=0
بما أن A هي مصفوفة فردية (المحدد هو 0)، وبالتالي فإن المعادلة ليس لها حل.
المثال رقم 3. يمارس. أوجد حل معادلة المصفوفة
حل. دعنا نشير إلى:
ثم ستكتب معادلة المصفوفة بالصيغة: X A = B.
محدد المصفوفة A هو detA=-60
بما أن A هي مصفوفة غير مفردة، فهناك مصفوفة معكوسة A -1 . لنضرب طرفي المعادلة على اليمين في A -1: X A A -1 = B A -1، حيث نجد أن X = B A -1
دعونا نجد المصفوفة العكسية A -1 .
المصفوفة المنقولة A T: 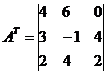
المصفوفة العكسية أ -1: 
نحن نبحث عن المصفوفة X باستخدام الصيغة: X = B A -1 
الجواب: > 
دعونا نحلل نوعين من الحلول لأنظمة المعادلات:
1. حل النظام باستخدام طريقة الاستبدال.
2. حل النظام عن طريق الجمع (الطرح) لمعادلات النظام حدًا تلو الآخر.
من أجل حل نظام المعادلات بطريقة الاستبدالتحتاج إلى اتباع خوارزمية بسيطة:
1. اكسبريس. من أي معادلة نعبر عن متغير واحد.
2. بديل. نعوض بالقيمة الناتجة في معادلة أخرى بدلاً من المتغير المعبر عنه.
3. حل المعادلة الناتجة بمتغير واحد. نجد حلا للنظام.
لتحل النظام عن طريق طريقة الجمع (الطرح) مصطلحًا تلو الآخربحاجة ل:
1. حدد المتغير الذي سنعمل له معاملات متطابقة.
2. نقوم بجمع أو طرح المعادلات، مما ينتج عنه معادلة ذات متغير واحد.
3. حل المعادلة الخطية الناتجة. نجد حلا للنظام.
حل النظام هو نقاط تقاطع الرسوم البيانية للوظائف.
دعونا نفكر بالتفصيل في حل الأنظمة باستخدام الأمثلة.
مثال 1:
دعونا نحل بطريقة الاستبدال
حل نظام المعادلات باستخدام طريقة الاستبدال2x+5y=1 (معادلة واحدة)
x-10y=3 (المعادلة الثانية)
1. اكسبريس
ويمكن ملاحظة أنه يوجد في المعادلة الثانية متغير x بمعامل 1، مما يعني أنه من الأسهل التعبير عن المتغير x من المعادلة الثانية.
س=3+10ص
2. وبعد أن عبرنا عنها، نعوض بـ 3+10y في المعادلة الأولى بدلاً من المتغير x.
2(3+10ص)+5ص=1
3. حل المعادلة الناتجة بمتغير واحد.
2(3+10ص)+5ص=1 (افتح القوسين)
6+20ص+5ص=1
25ص=1-6
25ص=-5 |: (25)
ص=-5:25
ص=-0.2
حل نظام المعادلات هو نقاط تقاطع الرسوم البيانية، لذلك نحتاج إلى إيجاد x و y، لأن نقطة التقاطع تتكون من x و y.لنجد x، في النقطة الأولى التي عبرنا عنها نستبدل y.
س=3+10ص
س=3+10*(-0.2)=1
ومن المعتاد أن نكتب النقاط في المقام الأول نكتب المتغير x، وفي المركز الثاني المتغير y.
الجواب: (1؛ -0.2)
المثال رقم 2:
دعونا نحل باستخدام طريقة الجمع (الطرح) حدًا تلو الآخر.
حل نظام المعادلات باستخدام طريقة الجمع3x-2y=1 (معادلة واحدة)
2x-3y=-10 (المعادلة الثانية)
1. نختار متغيرًا، لنفترض أننا اخترنا x. في المعادلة الأولى، المتغير x له معامل 3، في الثانية - 2. نحن بحاجة إلى جعل المعاملات هي نفسها، ولهذا لدينا الحق في ضرب المعادلات أو القسمة على أي رقم. نضرب المعادلة الأولى في 2، والثانية في 3 ونحصل على المعامل الإجمالي 6.
3س-2ص=1 |*2
6س-4ص=2
2س-3ص=-10 |*3
6س-9ص=-30
2. اطرح الثانية من المعادلة الأولى للتخلص من المتغير x وحل المعادلة الخطية.
__6س-4ص=2
5ص=32 | :5
ص=6.4
3. ابحث عن x. نعوض بـ y الموجود في أي من المعادلات، دعنا نقول في المعادلة الأولى.
3س-2ص=1
3س-2*6.4=1
3س-12.8=1
3س=1+12.8
3x=13.8 |:3
س=4.6
ستكون نقطة التقاطع x=4.6؛ ص=6.4
الجواب: (4.6؛ 6.4)
هل تريد الاستعداد للامتحانات مجانا؟ مدرس على الانترنت مجانا. لا تمزح.
استخدام المعادلات منتشر على نطاق واسع في حياتنا. يتم استخدامها في العديد من العمليات الحسابية وبناء الهياكل وحتى الألعاب الرياضية. استخدم الإنسان المعادلات في العصور القديمة، ومنذ ذلك الحين زاد استخدامها. معادلات القوة أو المعادلات الأسية هي معادلات تكون فيها المتغيرات ذات قوى وأساسها رقم. على سبيل المثال:
حل المعادلة الأسية يتلخص في خطوتين بسيطتين إلى حد ما:
1. أنت بحاجة إلى التحقق مما إذا كانت أسس المعادلة على اليمين واليسار هي نفسها. إذا كانت الأسباب ليست واحدة، فإننا نبحث عن خيارات لحل هذا المثال.
2. بعد أن تصبح القواعد واحدة، نساوي الدرجات ونحل المعادلة الجديدة الناتجة.
لنفترض أن لدينا معادلة أسية بالشكل التالي:
يجدر البدء بحل هذه المعادلة بتحليل الأساس. الأساسان مختلفان - 2 و4، ولكن لحلهما نحتاج إلى أن تكونا متماثلتين، لذلك نقوم بتحويل 4 باستخدام الصيغة التالية -\[ (a^n)^m = a^(nm):\]
نضيف إلى المعادلة الأصلية:
لنخرجها من الأقواس \
دعونا نعرب \
وبما أن الدرجات واحدة، فإننا نتخلص منها:
إجابة: \
أين يمكنني حل معادلة أسية باستخدام أحد الحلول عبر الإنترنت؟
يمكنكم حل المعادلة على موقعنا https://site. سيسمح لك الحل المجاني عبر الإنترنت بحل المعادلات عبر الإنترنت بأي تعقيد في غضون ثوانٍ. كل ما عليك فعله هو ببساطة إدخال بياناتك في الحل. يمكنك أيضًا مشاهدة تعليمات الفيديو ومعرفة كيفية حل المعادلة على موقعنا. وإذا كان لا يزال لديك أسئلة، يمكنك طرحها في مجموعة VKontakte الخاصة بنا http://vk.com/pocketteacher. انضم إلى مجموعتنا، نحن سعداء دائمًا بمساعدتك.
1. الفأس 2 =0 – غير مكتمل معادلة من الدرجة الثانية (ب=0، ج=0 ). الحل: س=0. الجواب: 0.
حل المعادلات.
2x·(x+3)=6x-x 2 .
حل.دعونا نفتح الأقواس عن طريق الضرب 2xلكل مصطلح بين قوسين:
2x 2 +6x=6x-x 2 ; ننقل المصطلحات من الجانب الأيمن إلى اليسار:
2x 2 +6x-6x+x 2 =0; وهنا مصطلحات مماثلة:
3x 2 = 0، وبالتالي x = 0.
إجابة: 0.
ثانيا. الفأس 2 +بx=0 –غير مكتمل معادلة من الدرجة الثانية (ج = 0 ). الحل: x (ax+b)=0 → x 1 =0 أو ax+b=0 → x 2 =-b/a. الجواب: 0؛ -ب/أ.
5س2 -26س=0.
حل.دعونا نخرج العامل المشترك Xخارج الأقواس:
س(5س-26)=0; كل عامل يمكن أن يساوي الصفر:
س = 0أو 5س-26=0→ 5س=26، اقسم طرفي المساواة على 5 ونحصل على: س=5.2.
إجابة: 0; 5,2.
مثال 3. 64س+4س2 =0.
حل.دعونا نخرج العامل المشترك 4xخارج الأقواس:
4س(16+س)=0. لدينا ثلاثة عوامل، 4≠0، أو س = 0أو 16+س=0. من المساواة الأخيرة نحصل على x=-16.
إجابة: -16; 0.
مثال 4.(س-3) 2 +5س=9.
حل.بتطبيق صيغة مربع الفرق بين تعبيرين، سنفتح الأقواس:
س 2 -6س+9+5س=9; تحويل إلى النموذج: x 2 -6x+9+5x-9=0; دعونا نقدم مصطلحات مماثلة:
س 2 -س=0; سوف نخرجها Xخارج الأقواس نحصل على: x (x-1)=0. من هنا أو س = 0أو س-1=0→ س=1.
إجابة: 0; 1.
ثالثا. الفأس 2 +ج=0 –غير مكتمل معادلة من الدرجة الثانية (ب=0 ); الحل: الفأس 2 =-ج → × 2 =-ج/أ.
لو (-ج/أ)<0 إذن لا توجد جذور حقيقية. لو (-س/أ)>0
مثال 5.× 2 -49=0.
حل.
× 2 = 49، من هنا س=±7. إجابة:-7; 7.
مثال 6. 9×2 -4=0.
حل.

غالبًا ما تحتاج إلى إيجاد مجموع المربعات (x 1 2 +x 2 2) أو مجموع المكعبات (x 1 3 +x 2 3) لجذور المعادلة التربيعية، وفي كثير من الأحيان - مجموع القيم المتبادلة من مربعات الجذور أو مجموع الجذور التربيعية الحسابية لجذور المعادلة التربيعية:
![]()
يمكن أن تساعد نظرية فييتا في هذا:
س 2 +بكسل+ف=0
x 1 + x 2 = -p; × 1 ∙ × 2 = ف.
دعونا نعرب خلال صو س:
1) مجموع مربعات جذور المعادلة س 2 +بكسل+ف=0;
2) مجموع مكعبات جذور المعادلة س 2 +بكسل+ف=0.
حل.
1) تعبير × 1 2 + × 2 2تم الحصول عليها عن طريق تربيع طرفي المعادلة x 1 + x 2 = -p;
(س 1 + س 2) 2 =(-ع) 2 ; افتح الأقواس: x 1 2 +2x 1 x 2 + x 2 2 =p 2 ; نعبر عن المبلغ المطلوب: x 1 2 + x 2 2 =p 2 -2x 1 x 2 =p 2 -2q. لقد حصلنا على مساواة مفيدة: س 1 2 + س 2 2 = ع 2 -2ق.
2) تعبير × 1 3 + × 2 3دعونا نمثل مجموع المكعبات باستخدام الصيغة:
(x 1 3 +x 2 3)=(x 1 +x 2)(x 1 2 -x 1 x 2 +x 2 2)=-ص·(ص 2 -2q-q)=-ص·(ص 2) -3ق).
معادلة أخرى مفيدة: س 1 3 + س 2 3 = -ص·(ص 2 -3ف).
أمثلة.
3) × 2 -3س-4=0.بدون حل المعادلة، احسب قيمة التعبير × 1 2 + × 2 2.
حل.
س 1 + س 2 = - ع = 3،والعمل × 1 ∙ × 2 = ف=في المثال 1) المساواة:
س 1 2 + س 2 2 = ع 2 -2ق.لدينا -ص=س 1 +س 2 = 3 → ص 2 =3 2 =9؛ س=× 1 × 2 = -4. ثم × 1 2 +x 2 2 =9-2·(-4)=9+8=17.
إجابة:س 1 2 + س 2 2 = 17.
4) س 2 -2س-4=0.احسب: x 1 3 +x 2 3 .
حل.
بواسطة نظرية فييتا، مجموع جذور هذه المعادلة التربيعية المختزلة هو س 1 + س 2 = - ع = 2،والعمل × 1 ∙ × 2 = ف=-4. فلنطبق ما تلقيناه ( في المثال 2) المساواة: س 1 3 + س 2 3 =-ص·(ع 2 -3ف)= 2·(2 2 -3·(-4))=2·(4+12)=2·16=32.
إجابة: س 1 3 + س 2 3 =32.
سؤال: ماذا لو أعطينا معادلة تربيعية غير مختزلة؟ الإجابة: يمكن دائمًا "تخفيضها" عن طريق قسمة حد على حد على المعامل الأول.
5) 2س2 -5س-7=0.دون أن تقرر، احسب: × 1 2 + × 2 2.
حل.لقد حصلنا على معادلة تربيعية كاملة. اقسم طرفي المساواة على 2 (المعامل الأول) واحصل على المعادلة التربيعية التالية: × 2 -2.5س-3.5=0.
وفقًا لنظرية فييتا، فإن مجموع الجذور يساوي 2,5 ; حاصل ضرب الجذور متساوي -3,5 .
نحن نحلها بنفس الطريقة كما في المثال 3) باستخدام المساواة: س 1 2 + س 2 2 = ع 2 -2ق.
س 1 2 + س 2 2 = ع 2 -2س= 2,5 2 -2∙(-3,5)=6,25+7=13,25.
إجابة: س 1 2 + س 2 2 = 13,25.
6) × 2 -5س-2=0.يجد:
دعونا نحول هذه المساواة، وباستخدام نظرية فييتا، نعوض عن مجموع الجذور -ص، ونتاج الجذور من خلال س، نحصل على صيغة مفيدة أخرى. عند اشتقاق الصيغة، استخدمنا المساواة 1): س 1 2 + س 2 2 = ع 2 -2ق.
في مثالنا س 1 + س 2 =-ص=5; × 1 ∙ × 2 = ف=-2. نستبدل هذه القيم في الصيغة الناتجة:

7) × 2 -13س+36=0.يجد:
دعونا نحول هذا المجموع ونحصل على صيغة يمكن استخدامها لإيجاد مجموع الجذور التربيعية الحسابية من جذور المعادلة التربيعية.
لدينا س 1 + س 2 =-ص=13; × 1 ∙ × 2 = ف = 36. نستبدل هذه القيم في الصيغة الناتجة:
نصيحة : تحقق دائمًا من إمكانية إيجاد جذور المعادلة التربيعية باستخدام الطريقة المناسبة، لأن 4 تمت مراجعته صيغ مفيدةتسمح لك بإكمال المهمة بسرعة، خاصة في الحالات التي يكون فيها المميز رقمًا "غير مناسب". في جميع الحالات البسيطة، ابحث عن الجذور وقم بالعمل عليها. على سبيل المثال، في المثال الأخير نحدد الجذور باستخدام نظرية فييتا: يجب أن يكون مجموع الجذور مساويًا لـ 13 ، ونتاج الجذور 36 . ما هي هذه الأرقام؟ بالتأكيد، 4 و 9.الآن احسب مجموع الجذور التربيعية لهذه الأرقام: 2+3=5. هذا كل شيء!
I. نظرية فييتاللمعادلة التربيعية المخفضة.
مجموع جذور المعادلة التربيعية المختزلة س 2 +بكسل+ف=0يساوي المعامل الثاني المأخوذ بالإشارة المعاكسة، وحاصل ضرب الجذور يساوي الحد الحر:
x 1 + x 2 = -p; × 1 ∙ × 2 = ف.
أوجد جذور المعادلة التربيعية المعطاة باستخدام نظرية فييتا.
مثال 1) × 2 -س-30=0.هذه هي المعادلة التربيعية المخفضة ( × 2 +بكسل+ف=0)، المعامل الثاني ع=-1، والعضو الحر س=-30.أولاً، دعونا نتأكد من أن هذه المعادلة لها جذور، وأن الجذور (إن وجدت) سيتم التعبير عنها بأعداد صحيحة. للقيام بذلك، يكفي أن يكون المميز مربعًا كاملاً لعدد صحيح.
إيجاد التمييز د=ب 2 — 4ج=(-1) 2 -4∙1∙(-30)=1+120=121= 11 2 .
الآن، وفقًا لنظرية فييتا، يجب أن يكون مجموع الجذور مساويًا للمعامل الثاني المأخوذ بالإشارة المعاكسة، أي. ( -ص)، والحاصل يساوي الحد الحر، أي. ( س). ثم:
س 1 + س 2 =1؛ × 1 ∙ × 2 = -30.علينا اختيار رقمين بحيث يكون حاصل ضربهما يساوي -30 ، والمبلغ هو وحدة. هذه أرقام -5 و 6 . الجواب: -5؛ 6.
مثال 2) × 2 +6س+8=0.لدينا المعادلة التربيعية المخفضة مع المعامل الثاني ع = 6وعضو حر س=8. دعونا نتأكد من وجود جذور صحيحة. دعونا نجد المميز د 1 د 1=3 2 -1∙8=9-8=1=1 2 . المميز D 1 هو المربع الكامل للرقم 1 مما يعني أن جذور هذه المعادلة هي أعداد صحيحة. دعونا نحدد الجذور باستخدام نظرية فييتا: مجموع الجذور يساوي –ص=-6، وحاصل ضرب الجذور يساوي س=8. هذه أرقام -4 و -2 .
في الواقع: -4-2=-6=-Р; -4∙(-2)=8=ف. الجواب: -4؛ -2.
مثال 3) × 2 +2س-4=0. في هذه المعادلة التربيعية المخفضة، المعامل الثاني ع = 2، والعضو الحر س=-4. دعونا نجد المميز د 1لأن المعامل الثاني هو عدد زوجي. د 1=1 2 -1∙(-4)=1+4=5. المميز ليس مربعًا كاملاً للعدد، لذلك نفعل ذلك خاتمة: جذور هذه المعادلة ليست أعدادًا صحيحة ولا يمكن إيجادها باستخدام نظرية فييتا.وهذا يعني أننا نحل هذه المعادلة، كالعادة، باستخدام الصيغ (في هذه الحالة، باستخدام الصيغ). نحن نحصل:
مثال 4).اكتب معادلة تربيعية باستخدام جذورها if × 1 = -7، × 2 = 4.
حل.سيتم كتابة المعادلة المطلوبة على الشكل: س 2 +بكسل+ف=0، وعلى أساس نظرية فييتا -ع=س 1 + س 2=-7+4=-3 → ع = 3؛ ف=س 1 ∙س 2=-7∙4=-28 . عندها ستأخذ المعادلة الشكل: × 2 +3س-28=0.
مثال 5).اكتب معادلة تربيعية باستخدام جذورها إذا:

ثانيا. نظرية فييتاللحصول على معادلة تربيعية كاملة الفأس 2 +بx+ج=0.
مجموع الجذور ناقص ب، مقسمة على أ، منتج الجذور يساوي مع، مقسمة على أ:
س 1 + س 2 = -ب/أ؛ س 1 ∙ س 2 = ج/أ.
مثال 6).أوجد مجموع جذور المعادلة التربيعية 2س2 -7س-11=0.
حل.
نتأكد من أن هذه المعادلة سيكون لها جذور. للقيام بذلك، يكفي إنشاء تعبير للمتميز، وبدون حسابه، فقط تأكد من أن المميز أكبر من الصفر. د=7 2 -4∙2∙(-11)>0 . الآن دعونا نستخدم نظرية فيتاللمعادلات التربيعية الكاملة.
س 1 + س 2 = -ب:أ=- (-7):2=3,5.
مثال 7). أوجد حاصل ضرب جذور المعادلة التربيعية 3x2 +8x-21=0.
حل.
دعونا نجد المميز د 1، منذ المعامل الثاني ( 8 ) هو رقم زوجي. د 1=4 2 -3∙(-21)=16+63=79>0 . المعادلة التربيعية لديها 2 الجذر، وفقًا لنظرية فييتا، هو حاصل ضرب الجذور × 1 ∙ × 2 = ج:أ=-21:3=-7.
I. الفأس 2 +bx+c=0- المعادلة التربيعية العامة
مميز د=ب 2 - 4أ.
لو د > 0إذن لدينا جذرين حقيقيين:
لو د = 0، إذن لدينا جذر واحد (أو جذرين متساويين) س=-ب/(2أ).
إذا د<0, то действительных корней нет.
مثال 1) 2س2 +5س-3=0.
حل. أ=2; ب=5; ج=-3.
د=ب 2 - 4أ=5 2 -4∙2∙(-3)=25+24=49=7 2 >0; 2 جذور حقيقية
4x2 +21x+5=0.
حل. أ=4; ب=21; ج=5.
د=ب 2 - 4أ=21 2 - 4∙4∙5=441-80=361=19 2 >0; 2 جذور حقيقية
ثانيا. الفأس 2 +بx+ج=0 – معادلة تربيعية ذات شكل معين مع حتى الثانية
معامل في الرياضيات او درجة ب

مثال 3) 3س2 -10س+3=0.
حل. أ=3; ب=-10 (رقم زوجي)؛ ج=3.

مثال 4) 5س2 -14س-3=0.
حل. أ=5; ب= -14 (رقم زوجي)؛ ج=-3.

مثال 5) 71x2 +144x+4=0.
حل. أ=71; ب=144 (رقم زوجي)؛ ج=4.

مثال 6) 9x 2 -30x+25=0.
حل. أ=9; ب=-30 (رقم زوجي)؛ ج=25.

ثالثا. الفأس 2 +بx+ج=0 – معادلة من الدرجة الثانية النوع الخاص المقدم: أ-ب+ج=0.
الجذر الأول يساوي دائمًا سالب واحد، والجذر الثاني يساوي دائمًا سالب مع، مقسمة على أ:
س 1 =-1، س 2 =-ج/أ.
مثال 7) 2x2 +9x+7=0.
حل. أ=2; ب=9; ج=7. دعونا نتحقق من المساواة: أ-ب+ج=0.نحن نحصل: 2-9+7=0 .
ثم × 1 =-1، × 2 =-ج/أ=-7/2=-3.5.إجابة: -1; -3,5.
رابعا. الفأس 2 +بx+ج=0 – معادلة تربيعية ذات شكل معين تخضع ل : أ+ب+ج=0.
الجذر الأول يساوي دائمًا واحدًا، والجذر الثاني يساوي دائمًا مع، مقسمة على أ:
× 1 = 1، × 2 = ج/أ.
مثال 8) 2س2 -9س+7=0.
حل. أ=2; ب=-9; ج=7. دعونا نتحقق من المساواة: أ+ب+ج=0.نحن نحصل: 2-9+7=0 .
ثم × 1 =1، × 2 = ج/أ=7/2=3.5.إجابة: 1; 3,5.
الصفحة 1 من 1 1

