Téměř celý kurz matematiky je založen na operacích s kladnými a zápornými čísly. Jakmile totiž začneme studovat souřadnicovou linii, začnou se všude, v každém novém tématu, objevovat čísla se znaménkem plus a mínus. Není nic jednoduššího než sečíst obyčejná kladná čísla, není těžké jedno od druhého odečítat. Dokonce i aritmetika se dvěma zápornými čísly je zřídka problém.

Mnoho lidí je však zmateno sčítáním a odečítáním čísel s různými znaménky. Připomeňme si pravidla, podle kterých k těmto akcím dochází.

Sčítání čísel s různými znaménky

Pokud k vyřešení problému potřebujeme přidat záporné číslo „-b“ k nějakému číslu „a“, musíme postupovat následovně.

• Vezměme moduly obou čísel - |a| a |b| - a porovnat tyto absolutní hodnoty mezi sebou.
• Všimněme si, který modul je větší a který menší, a odečteme menší hodnotu od větší hodnoty.
• Před výsledné číslo dáme znaménko čísla, jehož modul je větší.

To bude odpověď. Můžeme to vyjádřit jednodušeji: pokud je ve výrazu a + (-b) modul čísla „b“ větší než modul „a“, odečteme „a“ od „b“ a dáme „mínus “ před výsledkem. Pokud je modul „a“ větší, pak se „b“ odečte od „a“ - a řešení se získá se znaménkem „plus“.

Stává se také, že se moduly ukáží jako rovnocenné. Pokud ano, pak se na tomto místě můžeme zastavit – mluvíme o opačných číslech a jejich součet bude vždy roven nule.

Odečítání čísel s různými znaménky

Zabývali jsme se sčítáním, nyní se podíváme na pravidlo pro odčítání. Je to také docela jednoduché - a navíc úplně opakuje podobné pravidlo pro odečítání dvou záporných čísel.

Aby bylo možné od určitého čísla „a“ - libovolného, ​​tedy s jakýmkoli znaménkem - odečíst záporné číslo „c“, musíte k našemu libovolnému číslu „a“ přidat číslo opačné k „c“. Například:

• Pokud je „a“ kladné číslo a „c“ je záporné a potřebujete odečíst „c“ od „a“, zapíšeme to takto: a – (-c) = a + c.
• Pokud je „a“ záporné číslo a „c“ je kladné a „c“ je třeba od „a“ odečíst, zapíšeme jej následovně: (- a)– c = - a+ (-c).

Při odčítání čísel s různými znaménky se tedy nakonec vrátíme k pravidlům sčítání a při sčítání čísel s různými znaménky se vrátíme k pravidlům odčítání. Zapamatování těchto pravidel vám umožňuje rychle a snadno řešit problémy.

V tomto článku se podíváme na to, jak se to dělá odečtením záporných čísel z libovolných čísel. Zde uvedeme pravidlo pro odečítání záporných čísel a zvážíme příklady použití tohoto pravidla.

Navigace na stránce.

Pravidlo pro odečítání záporných čísel

Nastane následující pravidlo pro odečítání záporných čísel: abyste od čísla odečetli záporné číslo b, musíte k minuendu a přičíst číslo −b, které je naproti podbodu b.

V doslovné podobě pravidlo pro odečtení záporného čísla b od libovolného čísla a vypadá takto: a−b=a+(−b) .

Dokažme platnost tohoto pravidla pro odečítání čísel.

Nejprve si připomeňme význam odečítání čísel a a b. Najít rozdíl mezi čísly a a b znamená najít číslo c, jehož součet s číslem b je roven a (viz souvislost odčítání a sčítání). To znamená, že pokud se najde číslo c takové, že c+b=a, pak se rozdíl a−b rovná c.

K prokázání uvedeného pravidla odčítání tedy stačí ukázat, že přičtením čísla b k součtu a+(−b) dostaneme číslo a. Abychom to ukázali, pojďme se obrátit na vlastnosti operací s reálnými čísly. Díky kombinační vlastnosti sčítání platí rovnost (a+(−b))+b=a+((−b)+b). Protože součet opačných čísel je roven nule, pak a+((−b)+b)=a+0 a součet a+0 je roven a, protože přidání nuly číslo nezmění. Je tedy prokázána rovnost a−b=a+(−b), což znamená, že byla prokázána i platnost daného pravidla pro odečítání záporných čísel.

Toto pravidlo jsme dokázali pro reálná čísla a a b. Toto pravidlo však platí i pro libovolná racionální čísla a a b, stejně jako pro libovolná celá čísla a a b, protože akce s racionálními a celými čísly mají také vlastnosti, které jsme použili v důkazu. Všimněte si, že pomocí analyzovaného pravidla můžete odečíst záporné číslo od kladného i záporného čísla a také od nuly.

Zbývá zvážit, jak se provádí odečítání záporných čísel pomocí pravidla analýzy.

Příklady odečítání záporných čísel

Uvažujme příklady odečítání záporných čísel. Začněme vyřešením jednoduchého příkladu, abychom pochopili všechny složitosti procesu, aniž bychom se museli obtěžovat výpočty.

Příklad.

Odečtěte záporné číslo −7 od záporného čísla −13.

Řešení.

Opačné číslo k subtrahendu −7 je číslo 7. Pak podle pravidla pro odečítání záporných čísel máme (−13)−(−7)=(−13)+7. Zbývá sečíst čísla s různými znaménky, dostaneme (−13)+7=−(13−7)=−6.

Zde je celé řešení: (−13)−(−7)=(−13)+7=−(13−7)=−6 .

Odpovědět:

(−13)−(−7)=−6 .

Odečítání záporných zlomků lze provést převodem na odpovídající zlomky, smíšená čísla nebo desetinná místa. Zde stojí za to začít, s jakými čísly je pohodlnější pracovat.

Příklad.

Odečtěte záporné číslo od 3.4.

Řešení.

Aplikujeme pravidlo pro odečítání záporných čísel, máme . Nyní nahraďte desetinný zlomek 3.4 smíšeným číslem: (viz převod desetinných zlomků na obyčejné zlomky), dostaneme . Zbývá provést sčítání smíšených čísel: .

Tím je odčítání záporného čísla od 3.4 dokončeno. Zde je krátké shrnutí řešení: .

Odpovědět:

.

Příklad.

Odečtěte záporné číslo −0.(326) od nuly.

Řešení.

Podle pravidla pro odečítání záporných čísel máme 0−(−0,(326))=0+0,(326)=0,(326) . Poslední přechod je platný díky vlastnosti sčítání čísla s nulou.

Pokud se do toho chystáte, znalost záporných čísel není nezbytnou dovedností nastoupit do 5. třídy fyzikální a matematické školy. Tím si to však značně usnadníte, což se ještě podepíše na celkovém výsledku. zahajovací olympiády.

Pojďme tedy začít.
Nejprve musíte pochopit, že existují čísla menší než nula, která se nazývají záporná: například jedna je menší než toto , o jednu jednotku méně než 1, pak , a pak atd. Každé přirozené číslo má svého „záporného bratra“, číslo, které po přičtení k původnímu číslu dává .

Všechna přirozená čísla, mínus přirozená čísla a 0 dohromady tvoří množinu celých čísel.

Sčítání a odčítání

Pokud si představíte číselnou řadu, pravidla snadno zvládnete sčítání a odečítání záporných čísel:


Nejprve najděte na řádku číslo, do kterého nebo od kterého budete odečítat/přičítat. Dále, pokud potřebujete:

1. Přidejte záporné číslo a poté se musíte přesunout doleva
2. Přidejte kladné číslo - posuňte se doprava
3. Odečíst záporné - přesunout doprava
4. Odečíst kladné - pohyb doleva

podle počtu jednotek, které přidáte/odečtete. Nové místo, kde se ocitnete, bude výsledkem operace.

Samozřejmě úkoly pro pro přijetí do 5. třídy Bude možné řešit bez použití záporných čísel, ale obecně to zlepší vaši matematickou úroveň. Časem si nebudete kreslit ani představovat číselnou osu, ale budete to dělat „automaticky“, ale proto stojí za to cvičit: vymyslete jakoukoli čísla (záporná nebo kladná) a zkuste je nejprve sečíst a poté odečíst. Opakováním tohoto cvičení jednou denně budete mít během pár dní pocit, že jste se úplně naučili sčítat a odečítat libovolná celá čísla.

Násobení a dělení

Zde je situace ještě jednodušší: stačí si pamatovat, jak se znaménka mění při násobení nebo dělení:

Místo slova „podle“ může být násobení nebo dělení.
Rozhodneme se pro znaménko a samotné číslo je výsledkem vynásobení nebo dělení původních čísel bez znamének, resp.

V tomto článku se podíváme na to, jak to udělat z libovolných čísel. Zde uvedeme pravidlo pro odečítání záporných čísel a zvážíme příklady použití tohoto pravidla.

Navigace na stránce.

Nastane následující pravidlo pro odečítání záporných čísel: abyste od čísla odečetli záporné číslo b, musíte k minuendu a přičíst číslo −b, které je naproti podbodu b.

V doslovné podobě pravidlo pro odečtení záporného čísla b od libovolného čísla a vypadá takto: a−b=a+(−b) .

Dokažme platnost tohoto pravidla pro odečítání čísel.

Nejprve si připomeňme význam odečítání čísel a a b. Najít rozdíl mezi čísly a a b znamená najít číslo c, jehož součet s číslem b je roven a (viz souvislost odčítání a sčítání). To znamená, že pokud se najde číslo c takové, že c+b=a, pak se rozdíl a−b rovná c.

K prokázání uvedeného pravidla odčítání tedy stačí ukázat, že přičtením čísla b k součtu a+(−b) dostaneme číslo a. Abychom to ukázali, pojďme se obrátit na vlastnosti operací s reálnými čísly. Díky kombinační vlastnosti sčítání je rovnost (a+(−b))+b=a+((−b)+b) pravdivá. Protože součet opačných čísel je roven nule, pak a+((−b)+b)=a+0 a součet a+0 je roven a, protože přidání nuly číslo nezmění. Je tedy prokázána rovnost a−b=a+(−b), což znamená, že byla prokázána i platnost daného pravidla pro odečítání záporných čísel.

Toto pravidlo jsme dokázali pro reálná čísla a a b. Toto pravidlo však platí i pro libovolná racionální čísla a a b, stejně jako pro libovolná celá čísla a a b, protože akce s racionálními a celými čísly mají také vlastnosti, které jsme použili v důkazu. Všimněte si, že pomocí analyzovaného pravidla můžete odečíst záporné číslo jak od kladného čísla, tak od záporného čísla a také od nuly.

Zbývá zvážit, jak se provádí odečítání záporných čísel pomocí pravidla analýzy.

Příklady odečítání záporných čísel

Uvažujme příklady odečítání záporných čísel. Začněme vyřešením jednoduchého příkladu, abychom pochopili všechny složitosti procesu, aniž bychom se museli obtěžovat výpočty.

Odečtěte záporné číslo −7 od záporného čísla −13.

Opačné číslo k subtrahendu −7 je číslo 7. Pak podle pravidla pro odečítání záporných čísel máme (−13)−(−7)=(−13)+7. Zbývá sečíst čísla s různými znaménky, dostaneme (−13)+7=−(13−7)=−6.

Zde je celé řešení: (−13)−(−7)=(−13)+7=−(13−7)=−6 .

Odečítání záporných zlomků lze provést změnou na odpovídající zlomky, smíšená čísla nebo desetinná místa. Zde stojí za to začít, s jakými čísly je pohodlnější pracovat.

Odečtěte záporné číslo od 3.4.

Aplikujeme pravidlo pro odečítání záporných čísel, máme . Nyní nahraďte desetinný zlomek 3.4 smíšeným číslem: (viz převod desetinných zlomků na obyčejné zlomky), dostaneme . Zbývá provést sčítání smíšených čísel: .

Tím je odčítání záporného čísla od 3.4 dokončeno. Zde je krátké shrnutí řešení: .

.

Odečítání záporných čísel

Jak víte, odčítání je opakem sčítání.

Pokud jsou „a“ a „b“ kladná čísla, pak odečtením čísla „b“ od čísla „a“ se zjistí číslo „c“, které po sečtení „s“ s číslem „b“ dává číslo „a“. “.

Definice odčítání platí pro všechna racionální čísla. To znamená odečítání kladných a záporných čísel lze nahradit přidáním.

Chcete-li od jednoho čísla odečíst další, musíte přidat opačné číslo k tomu, které se odečítá.

Nebo jiným způsobem můžeme říci, že odečítání čísla „b“ je stejné jako sčítání, ale s číslem opačným k číslu „b“.

Stojí za to si zapamatovat níže uvedené výrazy.

Pravidla pro odečítání záporných čísel

Jak je vidět z výše uvedených příkladů, odečtení čísla „b“ je sčítání s číslem opačným k číslu „b“.

Toto pravidlo platí nejen při odečítání menšího čísla od většího, ale také umožňuje odečíst větší číslo od menšího čísla, to znamená, že vždy najdete rozdíl dvou čísel.

Rozdíl může být kladné číslo, záporné číslo nebo nula.

Příklady odečítání záporných a kladných čísel.

Pohodlné na zapamatování pravidlo znamení, což umožňuje snížit počet závorek.

Znaménko plus nemění znaménko čísla, takže pokud je před závorkou plus, znaménko v závorce se nemění.

Znaménko mínus před závorkou převrací znaménko čísla v závorce.

Z rovnosti je zřejmé, že pokud jsou před a uvnitř závorky shodná znaménka, dostaneme „+“, a pokud jsou znaménka různá, dostaneme „-“.

Pravidlo znamének platí i v případě, že závorky neobsahují pouze jedno číslo, ale algebraický součet čísel.

Upozorňujeme, že pokud je v závorkách několik čísel a před závorkami je znaménko mínus, musí se znaménka před všemi čísly v těchto závorkách změnit.

Abyste si zapamatovali pravidlo o znacích, můžete si vytvořit tabulku pro určování znamének čísla.

Pravidlo odečítání záporných čísel

Akce se zápornými a kladnými čísly

Absolutní hodnota (modul). Přidání.

Odčítání. Násobení. Divize.

Absolutní hodnota (modul). Pro záporné číslo– je kladné číslo získané změnou znaménka z „–“ na „+“; Pro kladné číslo a nula– to je samotné číslo. K označení absolutní hodnoty (modulu) čísla se používají dvě přímky, do kterých se toto číslo zapisuje.

PŘÍKLADY: | – 5 | = 5, | 7 | = 7, | 0 | = 0.

1) Při sčítání dvou čísel se stejnými znaménky se sčítají

jejich absolutní hodnoty a před součet se umístí společné znaménko.

2) Při sčítání dvou čísel s různými znaménky jsou jejich absolutní hodnoty

množství se odečte (od většího menšího) a vloží se znaménko

čísla s větší absolutní hodnotou.

Odčítání. Odečítání dvou čísel můžete nahradit sčítáním, ve kterém si minuend zachovává své znaménko a odčítání se bere s opačným znaménkem.

(+ 8) – (+ 5) = (+ 8) + (– 5) = 3;

(+ 8) – (– 5) = (+ 8) + (+ 5) = 13;

(– 8) – (– 5) = (– 8) + (+ 5) = – 3;

(– 8) – (+ 5) = (– 8) + (– 5) = – 13;

Násobení. Při násobení dvou čísel se jejich absolutní hodnoty vynásobí a součin získá znaménko „+“, pokud jsou znaménka faktorů stejná, a znaménko „–“, pokud se znaménka faktorů liší.

Následující schéma je užitečné ( pravidla násobení):

Při násobení několika čísel (dvě nebo více) má součin znaménko „+“, pokud je počet záporných faktorů sudý, a znaménko „–“, pokud je jejich počet lichý.

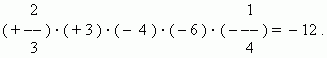
Divize. Při dělení dvou čísel se absolutní hodnota děliče vydělí absolutní hodnotou dělitele a podíl má znaménko „+“, pokud jsou znaménka děliče a dělitele stejná, a znaménko „–“, pokud jsou znaménka dividendy a dělitele se liší.

Jednat zde Stejný pravidla znamének jsou stejná jako pro násobení:

Sčítání a odečítání kladných a záporných čísel

Nerozumíte ničemu?

Zkuste požádat o pomoc učitele

Pravidlo pro sčítání záporných čísel

K sečtení dvou záporných čísel potřebujete:

• provést přidání jejich modulů;
• přidejte k přijaté částce znak „–“.

Podle pravidla sčítání můžeme psát:

Pravidlo pro sčítání záporných čísel platí pro záporná celá čísla, racionální čísla a reálná čísla.

Sečtěte záporná čísla $−185$ a $−23\789.$

Použijme pravidlo pro sčítání záporných čísel.

Pojďme najít moduly těchto čísel:

Sečteme výsledná čísla:

$185+23 \ 789=23 \ 974$.

Umístěte znak $“–“$ před nalezené číslo a získejte $-23 974 $.

Stručné řešení: $(−185)+(−23\789)=−(185+23\789)=−23\974$.

Při sčítání záporných racionálních čísel je třeba je převést do tvaru přirozených čísel, obyčejných nebo desetinných zlomků.

Sečtěte záporná čísla $-\frac $ a $-7,15$.

Podle pravidla pro sčítání záporných čísel musíte nejprve najít součet modulů:

Získané hodnoty je vhodné redukovat na desetinné zlomky a provést jejich sečtení:

Před výslednou hodnotu dáme znak $“–“$ a získáme –7,4 $.

Krátké shrnutí řešení:

Sčítání čísel s opačnými znaménky

Pravidlo pro sčítání čísel s opačnými znaménky:

• vypočítat moduly čísel;
• porovnejte výsledná čísla:

pokud se rovnají, pak jsou původní čísla opačná a jejich součet je nula;

pokud se nerovnají, musíte si zapamatovat znaménko čísla, jehož modul je větší;

• odečtěte menší od většího modulu;
• Před výslednou hodnotu vložte znaménko čísla, jehož modul je větší.

Sčítání čísel s opačnými znaménky znamená odečítání menšího záporného čísla od většího kladného čísla.

Pravidlo pro sčítání čísel s opačnými znaménky platí pro celá čísla, racionální a reálná čísla.

Sečtěte čísla $4$ a $-8$.

Musíte sečíst čísla s opačnými znaménky. Použijme odpovídající pravidlo sčítání.

Pojďme najít moduly těchto čísel:

Modul čísla $−8$ je větší než modul čísla $4$, tzn. zapamatujte si znak $“–“$.

Před výsledné číslo dáme znak $“–“$, který jsme si zapamatovali, a dostaneme $−4.$

Krátké shrnutí řešení:

Jste líní na čtení?

Zeptejte se odborníků a získejte
odpověď do 15 minut!

Chcete-li sečíst racionální čísla s opačnými znaménky, je vhodné je reprezentovat ve formě obyčejných nebo desetinných zlomků.

Odečítání záporných čísel

Pravidlo pro odečítání záporných čísel:

Abychom odečetli záporné číslo $b$ od čísla $a$, je nutné k minuendu $a$ přidat číslo $−b$, které je opakem subtrahendu $b$.

Podle pravidla odčítání můžeme psát:

Toto pravidlo platí pro celá čísla, racionální a reálná čísla. Pravidlo lze použít k odečtení záporného čísla od kladného čísla, od záporného čísla a od nuly.

Odečtěte záporné číslo $−5$ od záporného čísla $−28$.

Opačné číslo pro číslo $–5$ je číslo $5$.

Podle pravidla pro odečítání záporných čísel dostaneme:

Sečteme čísla s opačnými znaménky:

Při odečítání záporných zlomků musíte čísla převést na zlomky, smíšená čísla nebo desetinná místa.

Odečítání čísel s opačnými znaménky

Pravidlo pro odečítání čísel s opačnými znaménky je stejné jako pravidlo pro odečítání záporných čísel.

Odečtěte kladné číslo $7$ od záporného čísla $−11$.

Opakem 7 $ je $ – 7 $.

Podle pravidla pro odečítání čísel s opačnými znaménky dostaneme:

Sečteme záporná čísla:

Stručné řešení: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.

Při odečítání zlomkových čísel s opačnými znaménky je nutné čísla převést do tvaru obyčejných nebo desetinných zlomků.

Nikdy nenašel odpověď
na tvou otázku?

Stačí napsat, co potřebujete
je potřeba pomoc

Odečítání záporného čísla, pravidlo, příklady

Tento článek je věnován analýze takového tématu, jako je odečítání záporných čísel. Materiál poskytuje užitečné informace o pravidle pro odečítání záporných čísel a dalších definicích. Abychom posílili podstatu odstavce, podrobně rozebereme příklady typických cvičení a úkolů.

Pravidlo pro odečítání záporných čísel

Abyste tomuto tématu porozuměli, měli byste se naučit základní definice a pojmy.

Pravidlo pro odečítání záporných čísel je formulováno takto: tak, že z čísla A odečíst číslo b se znaménkem mínus, nutné snížit A přidejte číslo − b, které je opakem subtrahendu b .

Pokud si představíme toto pravidlo pro odečítání záporného čísla b z libovolného čísla a ve tvaru písmene, pak to bude vypadat takto: a − b = a + (− b) .

Pro použití tohoto pravidla je nutné prokázat jeho platnost.

Vezměme si čísla A A b. Odečíst od čísla Ačíslo b, musíte takové číslo najít S, který se sčítá s číslem b se bude rovnat číslu A. Jinými slovy, pokud se takové číslo najde C, Co c + b = a, pak ten rozdíl a − b rovná C .

Abychom dokázali pravidlo odčítání, je nutné ukázat, že sčítání součtu a + (− b) s číslem b- toto je číslo A. Je nutné si zapamatovat vlastnosti operací s reálnými čísly. Protože v tomto případě funguje kombinační vlastnost sčítání, rovnost (a + (− b)) + b = a + ((− b) + b) bude pravda.

Protože součet čísel s opačnými znaménky je roven nule, pak a + ((− b) + b) = a + 0 a součet a + 0 = a ( Pokud k číslu přidáte nulu, nezmění se). Rovnost a − b = a + (− b) je považován za prokázaný, což znamená, že je prokázána i platnost daného pravidla pro odečítání čísel se znaménkem mínus.

Podívali jsme se, jak toto pravidlo funguje pro reálná čísla A A b. Ale je také považován za platný pro všechna racionální a celá čísla A A b. Vlastnosti použité v důkazu mají i operace s racionálními a celými čísly. Je třeba dodat, že pomocí parsovaného pravidla můžete provádět akce čísla se znaménkem mínus jak od kladného čísla, tak od záporného čísla nebo nuly.

Podívejme se na analyzované pravidlo na typických příkladech.

Příklady použití pravidla odčítání

Podívejme se na příklady zahrnující odečítání čísel. Nejprve se podívejme na jednoduchý příklad, který vám pomůže snadno pochopit všechny složitosti procesu.

Musí se odečíst od čísla − 13 číslo − 7 .

Vezměme opačné číslo, které se má odečíst − 7 . Tohle číslo 7 . Pak podle pravidla pro odečítání záporných čísel máme (− 13) − (− 7) = (− 13) + 7 . Udělejme sčítání. Nyní dostáváme: (− 13) + 7 = − (13 − 7) = − 6 .

Zde je celé řešení: (− 13) − (− 7) = (− 13) + 7 = − (13 − 7) = − 6 . (− 13) − (− 7) = − 6 . Lze také provést odečítání zlomkových záporných čísel. Musíte přejít na zlomky, smíšená čísla nebo desetinná místa. Výběr čísla závisí na tom, se kterou možností je pro vás pohodlnější pracovat.

Musíte odečíst od čísla 3 , 4 čísla - 23 2 3 .

Aplikujeme výše popsané pravidlo odčítání, dostaneme 3, 4 - - 23 2 3 = 3, 4 + 23 2 3. Zlomek nahradíme desetinným číslem: 3, 4 = 34 10 = 17 5 = 3 2 5 (jak překládat zlomky můžete vidět v materiálu k tématu), dostaneme 3, 4 + 23 2 3 = 3 2 5 + 23 2 3. Udělejme sčítání. Tím je odčítání záporného čísla - 23 2 3 dokončeno 3 , 4 dokončeno.

Zde je krátké shrnutí řešení: 3, 4 - - 23 2 3 = 27 1 15.

Musíte odečíst číslo − 0 , (326) od nuly.

Podle pravidla odčítání, které jsme se naučili výše, 0 − (− 0 , (326)) = 0 + 0 , (326) = 0 , (326) .

Poslední přechod je správný, protože zde funguje vlastnost přidání čísla s nulou: 0 − (− 0 , (326)) = 0 , (326) .

Z probraných příkladů je zřejmé, že při odečítání záporného čísla můžete získat kladné i záporné číslo. Odečtením záporného čísla může vzniknout číslo 0 , to se stane, když se minuend rovná subtrahendu.

Je nutné vypočítat rozdíl záporných čísel - 5 - - 5.

Pravidlem odčítání dostaneme - 5 - - 5 = - 5 + 5.

Dospěli jsme k součtu opačných čísel, který je vždy roven nule: - 5 - - 5 = - 5 + 5 = 0

V některých případech musí být výsledek odčítání zapsán jako číselný výraz. To platí v případech, kdy minuend nebo subtrahend je iracionální číslo. Například odečítání od záporného čísla − 2 záporné číslo – π proveden takto: (− 2) − (− π) = (− 2) + π = π − 2. Hodnotu výsledného výrazu lze vypočítat co nejpřesněji pouze v případě potřeby. Pro podrobné informace si můžete prostudovat další sekce související s tímto tématem.

Nyní se podíváme na příklady odečtením záporných čísel, a uvidíte, že je to velmi snadné. Stačí si zapamatovat pravidlo: dvě mínus vedle sebe dávají plus.

Příklad 1: Odečtení záporného čísla od kladného čísla

56 – (–34) = 56 + 34 = 90

Jak můžete vidět, abyste odečetli záporné číslo od kladného čísla, musíte jednoduše přidat jejich moduly.

Příklad 2: Odečtení záporného čísla od záporného čísla

– 60 – (– 25) = – 60 + 25 = – 35

– 15 – (– 30) = – 15 + 30 = 15

Při odečítání záporného čísla od záporného se tedy řídíme pravidlem a můžeme skončit s kladným i záporným číslem.

Existuje jediné pravidlo, kterým se řídí odečítání libovolných čísel: záporných i kladných, a zní takto:

Pravidlo znamení

Abychom se zbavili nadbytečných závorek při odečítání záporných čísel, můžeme použít pravidlo znaménka.Toto pravidlo říká:

Například:

Nyní si udělejte test a otestujte se!

Sčítání a odečítání záporných čísel

Časový limit: 0

Navigace (pouze čísla úloh)

0 z 20 dokončených úkolů